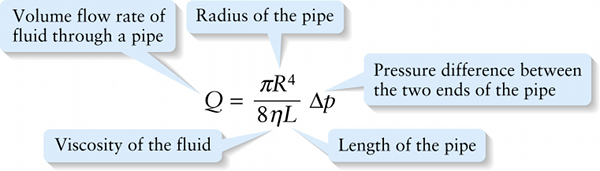
Chapter 11. Hagen-Poiseuille equation for laminar flow of a viscous fluid (11-30)
Question
9GrTdGNwdhJOEL64DwKJIW7MFAKtex4e4qcp5Xak7tcG+GR14O8+ORksxG4=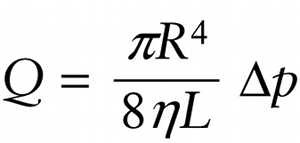
Question
2mvniaXc/+/TC40tV0sifT8oYGvgVKZo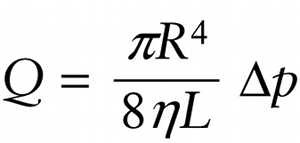
Question
ms+db4WGqVfDXbBXWWUE2sbvA1QlB09Q/7CuhsoA+JAbyMxkotevb7iChjcy1Iwr44LDPhbzQss=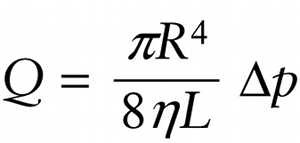
Question
N4Q8mtAOE83fVk97QifbcBOOgHkRpXLc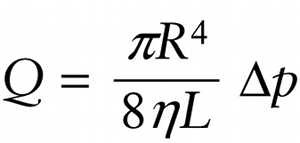
Question
Ki0EyvefEUoQ10/GAwW63As4dii6L7f0sZnztQ==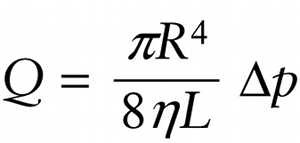
Review
Figure 11-36 shows the laminar flow of fluid within a circular pipe seen in cross section. Due to friction, the fluid that’s right up against the inside walls of the pipe doesn’t move at all. This is the \(\textit{no-slip condition}\) that we described in Section 11-9. (The fluid in contact with the lower plate in Figure 11-34 behaved the same way.) The fluid a small distance from the walls moves a little, the fluid a bit farther away moves a bit faster, and so on. The fastest flow is at the very center of the pipe. This flow pattern is called \(\textit{parabolic}\) (since the dashed curve in Figure 11-36 is a parabola lying on its side). A derivation using calculus gives the following expression, called the \(\textbf{Hagen-Poiseuille equation}\), relating the pressure difference between the two ends of the pipe to the resulting flow rate. (Non-French speakers can pronounce Poiseuille as “pwa-zoo-yah.”)