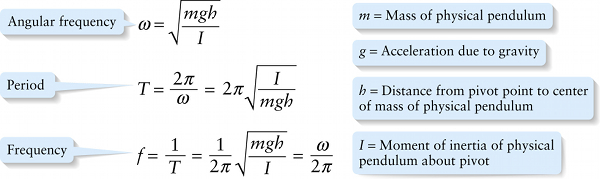Chapter 12. Angular frequency, period, and frequency for a physical pendulum (small amplitude) (12-31)
Question
74ZQsRWNs5eaxFMtu1ST1zsHSXQD2A/8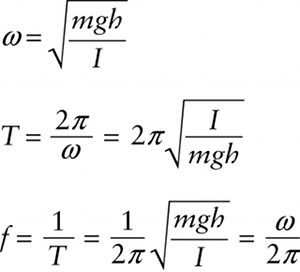
Question
i3GYZUGh83sgFQrZ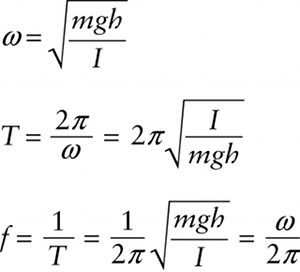
Question
6AjRK1rC+/08Tcq8CY6Akw==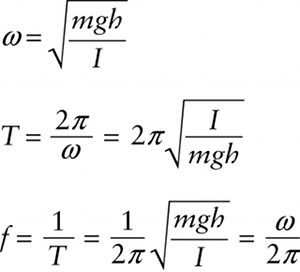
Review
Compare Equation 12-30 to the corresponding equation for the simple pendulum that we derived in Section 12-5, \(\alpha_z\approx -(g/L)\theta\) (Equation 12-26): The equation is identical except that \(g/L\) has been replaced by \(mgh/I\). So we conclude that just as for the simple pendulum, the oscillations of a physical pendulum are simple harmonic motion provided that the amplitude is relatively small. To find the angular frequency, period, and frequency of a physical pendulum, we simply take Equations 12-27 for a simple pendulum and replace \(g/L\) with \(mgh/I\):