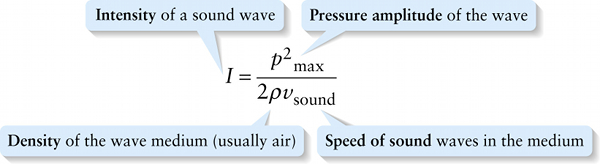
Chapter 13. Sound wave intensity in terms of pressure amplitude Pmax (13-31)
Question
I0ODsB/JtbEJyaEQ3jSbeivMBtSXR8cIIIt8zD5LOYXwbbRqjpHfllqhB4E=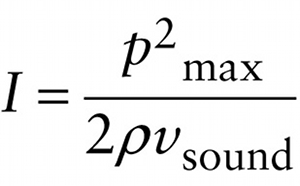
Question
gTvVLHTREsFG4FIU/+eCXuj/aGQ2PiHMb5sCZQ53AKJQDBereF9KrslJ3R5iclVK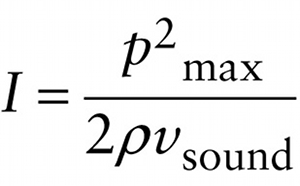
Question
kZbtO/SFxE5PzfTwwODYlyd3Na6MyS14r5p8tfkzYrwY2ZFDGgPPoLfQMyxOhEb38vXhB3xDR48UK0fcBvnx4g==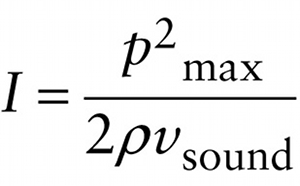
Question
3iGtWs7rexX3USNVoGOhCKzOI04eJfEDv0D6oW1yt74ZvVseUt98IkAB8Ob+KBqYJJOK+Si68lUxvaba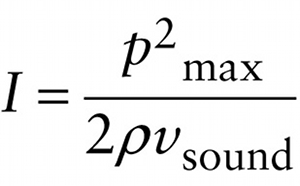
Review
Equation 13-29 is expressed in terms of the displacement amplitude A. However, our ears are more directly sensitive to the pressure variations in a sound wave. The displacement amplitude A in a sound wave is related to the pressure amplitude pmax, or maximum pressure variation, by
(13-30) \(A = \frac{p_{\mathrm{max}}}{\rho{v_{\mathrm{sound}}}\omega}\)
If we substitute Equation 13-30 for \(A\) into Equation 13-29, we get an alternative expression for the intensity of a sound wave:
\(I = \frac{1}{2}\rho{v_{\mathrm{sound}}\omega^2}\left(\frac{p_{\mathrm{max}}}{\rho{v_{\mathrm{sound}}}\omega}\right)^2 = \frac{p_{\mathrm{max}}^2}{2}\frac{\rho{v_{\mathrm{sound}}}\omega^2}{\rho^2v_{\mathrm{sound}}^2\omega^2}\)
or, simplifying,