Chapter 1. Impact 10.2
Impact…ON BIOCHEMISTRY: I10.2 Computational studies of biomolecules
Computational chemistry is commonly used to estimate standard enthalpies of formation (Topic 2C) of molecules with complex three-dimensional structures. The computational approach also makes it possible to gain insight into the effect of solvation on the enthalpy of formation without conducting experiments. A calculation performed in the absence of solvent molecules estimates the properties of the molecule of interest in the gas phase. Computational methods are available that allow for modelling the effect of solvent molecules around a solute molecule, thereby taking into account the effect of molecular interactions with the solvent on the enthalpy of formation of the solute. Again, the numerical results are only estimates and the primary purpose of the calculation is to predict whether interactions with the solvent increase or decrease the enthalpy of formation. As an example, consider the amino acid glycine, which can exist in a neutral (1) or zwitterionic (2) form, in which the amino group is protonated and the carboxyl group is deprotonated. It is possible to show computationally that in the gas phase the neutral form has a lower enthalpy of formation than the zwitterionic form. However, in water the opposite is true because of strong interactions between the polar solvent and the charges in the zwitterion.
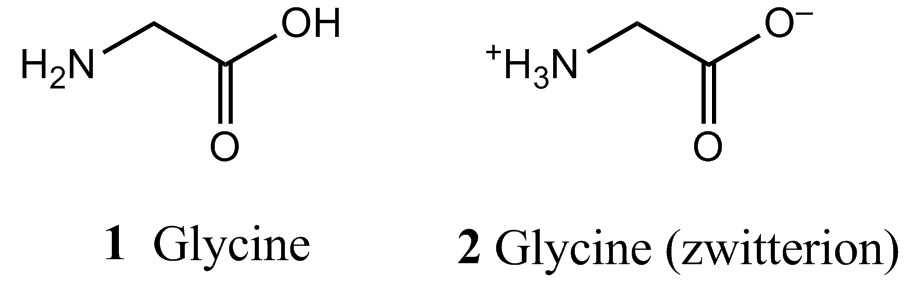
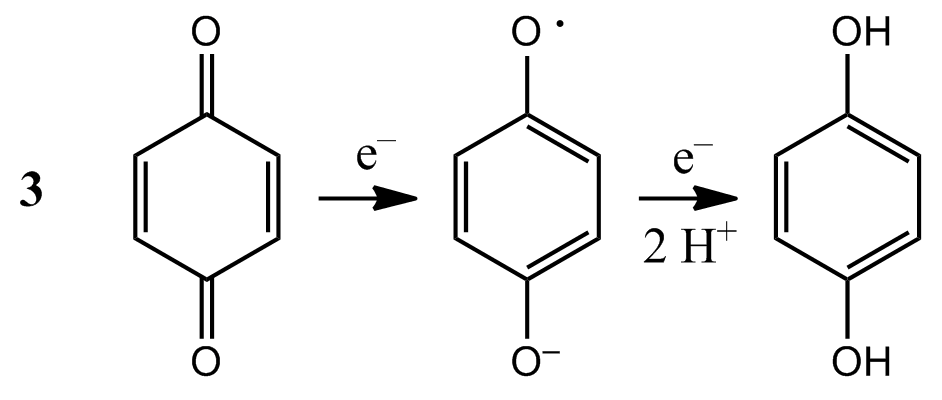
Molecular orbital calculations can also be used to predict trends in electrochemical properties, such as standard potentials (Topic 6D). Several experimental and computational studies of aromatic hydrocarbons indicate that decreasing the energy of the LUMO enhances the ability of a molecule to accept an electron into the LUMO, with an attendant increase in the value of the standard potential of the molecule. The effect is also observed in quinones and flavins, which are co-factors involved in biological electron transfer reactions. For example, stepwise substitution of the hydrogen atoms in p-benzoquinone by methyl groups (–CH3) results in a systematic increase in the energy of the LUMO and a decrease in the standard potential for formation of the semiquinone radical (3). The standard potentials of naturally occurring quinones are also modified by the presence of different substituents, a strategy that imparts specific functions to specific quinones. For example, the substituents in coenzyme Q are largely responsible for positioning its standard potential so that the molecule can function as an electron shuttle between specific electroactive proteins in the respiratory chain (Impact I6.1).
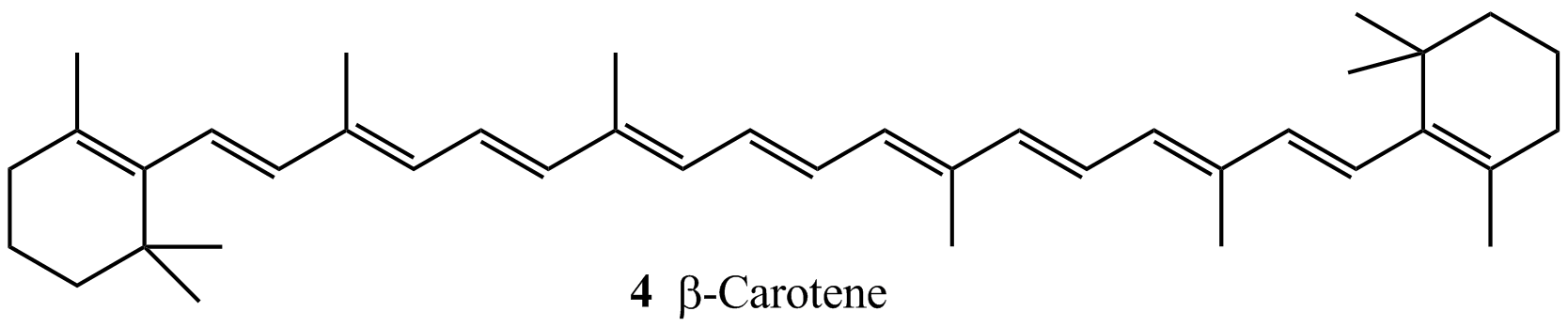
Calculations based on semi-empirical, ab initio, and DFT methods are used to the calculated HOMO–LUMO energy gaps with the wavelengths of spectroscopic absorptions. For example, consider the linear polyenes shown in Table I10.1: ethene (C2H4), butadiene (C4H6), hexatriene (C6H8), and octatetraene (C8H10), all of which absorb in the ultraviolet region of the spectrum. The table also shows that, as expected, the wavelength of the lowest-energy electronic transition decreases as the energy separation between the HOMO and LUMO increases. We also see that the smallest HOMO–LUMO gap and longest transition wavelength correspond to octatetraene, the longest polyene in the group. It follows that the wavelength of the transition increases with increasing number of conjugated double bonds in linear polyenes. Extrapolation of the trend suggests that a sufficiently long linear polyene should absorb light in the visible region of the electromagnetic spectrum. This is indeed the case for β-carotene (4), which absorbs light with λ ≈ 450 nm. The ability of β-carotene to absorb visible light is part of the strategy employed by plants to harvest solar energy for use in photosynthesis (Topic 20G).
| Polyene | { E(HOMO) – E(LUMO)}/eV | λ/nm |
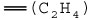 | 18.1 | 163 |
 | 14.5 | 217 |
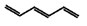 | 12.7 | 252 |
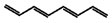 | 10.8 | 304 |