Chapter 1. The cross product
10.1 – Introduction to the cross product
The dot product, described in the previous tutorial, is only one way to multiply two vectors. We can also multiply two vectors \(\overrightarrow{A}\) and \(\overrightarrow{B}\) using the cross product.
This operation is written as
\(\overrightarrow{C} = \overrightarrow{A} \times \overrightarrow{B}\)
In the equation, the symbol “×” represents the mathematical operation known as the cross product.
Note: The result of taking the cross product of two vectors is another vector, whereas taking the dot product of two vectors (see tutorial 9) results in a scalar quantity.
The magnitude of the resulting vector from a cross product is equal to the product of the magnitudes of the two vectors and the sine of the angle between them.
So
\(C=| \overrightarrow{A} \times \overrightarrow{B}|=AB{\,}\mathtt{sin}\, \phi \)
The cross product of two vectors, \(\overrightarrow{A}\) and \(\overrightarrow{B}\) is always a vector perpendicular both \(\overrightarrow{A}\) and \(\overrightarrow{B}\), as we can see in the picture:
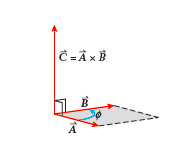
The cross product is a vector \(\overrightarrow{C}\) that is perpendicular to both \(\overrightarrow{A}\) and \(\overrightarrow{B}\), and has a magnitude AB sin ϕ, which equals the area of the parallelogram shown.
Note: The order of the two vectors in a cross product makes a difference. The cross product of \(\overrightarrow{B}\) and \(\overrightarrow{A}\) is the negative of the cross product of \(\overrightarrow{A}\) and \(\overrightarrow{B}\) or
\(\overrightarrow{A} \times \overrightarrow{B} = -\overrightarrow{B} \times \overrightarrow{A}\)
This results from the definition of the angle ϕ shown in the diagram - ϕ is directed from the first vector (\(\overrightarrow{A}\)) to the second vector (\(\overrightarrow{B}\)). If you travel the angle from the second vector to the first—in reverse direction, -ϕ becomes negative. The sine of a negative angle is also negative so calculating the cross product will give a negative answer.
Cross products are distributive, so \( \overrightarrow{A} \times ( \overrightarrow{B} + \overrightarrow{C}) = \overrightarrow{A} \times \overrightarrow{B} + \overrightarrow{A} \times \overrightarrow{C}\)
10.2 – Determining the direction of a cross product
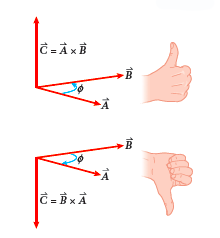
a cross product - Take a
minute to practice this
for \(\overrightarrow{A} \times \overrightarrow{B}\) and \(\overrightarrow{B} \times \overrightarrow{A}\). Do
you get opposite
directions for the \(\overrightarrow{C}\)vector?
To determine the direction of the cross product
\(\overrightarrow{C} = \overrightarrow{A} \times \overrightarrow{B}\), you can use the right-hand rule.
How to do it:
1. Point the fingers of your right hand in the direction of the first vector of the cross product (in this case \(\overrightarrow{A}\)).
2. Then curl your fingers toward the second vector, \(\overrightarrow{B}\). If you stick your thumb straight out, it points in the direction of the cross product, vector \(\overrightarrow{C}\) (the picture to the left may help).
If you instead want to find the direction of the cross product \(\overrightarrow{B} \times \overrightarrow{A}\), begin by pointing the fingers of your right hand in the direction of vector \(\overrightarrow{B}\). Then curl them toward vector \(\overrightarrow{A}\). Your thumb again points in the direction of the cross product.
Notice that using this method \(\overrightarrow{A} \times \overrightarrow{B}\) gives the opposite direction to \(\overrightarrow{B} \times \overrightarrow{A}\) as expected!
10.3 – The cross product – special cases
There are two special cases of the cross product that are worth pointing out.
1.The cross product of perpendicular vectors
In this case, the angle between the vectors, ϕ = 90°, so sin ϕ = 1
Therefore the magnitude of the cross product of perpendicular vectors is equal to:
\( |\overrightarrow{A} \times \overrightarrow{B}|=AB{\,}\mathtt{sin}{\,}90°=AB(1)=AB \)
2.The cross product of parallel vectors
In this case, the angle between the vectors, ϕ = 0°, so Sin ϕ = 0
Therefore the magnitude of the cross product of parallel vectors is equal to:
\( |\overrightarrow{A} \times \overrightarrow{B}|=AB{\,}\mathtt{sin}{\,}0=AB(0)=0 \)
One example of this is the cross product of a vector with itself, \(\overrightarrow{A} \times \overrightarrow{A}\) = 0.
Try it yourself 1
Evaluate the magnitude of the following cross products,
Question Sequence
Question 1.1
fY4hPY5tf3rubx0MIF3AqWSK4CA9xuNLt0K8OPx8hzdcM80N4k66ZqkGeLFQx/qkKnVx57wVVfxhV+r30DmmLoAQoT/sSSUOMabRbXZPnxvHBPhYbD/WvcLJRoTWx8zVq0QkZfZHPNTWBtfCkgXDn3E6QfJfzgxq2rNaZxVCvhb1TnB/XJcYRpHj2srNTACVo1CTBfep0gETyz84VBLudArRzYW7Ne6tZ+NQ0cBunlNBWX8hUfKxhHBH41l647eX3SzuuPgfZ5jMzcsTLiWaMw==Question 1.2
BM0UEIYSzsOKWgs2NNTdQimmjCVdODIA2QCBNZyAbGNJzVH4pyIkuhqlm8uXk/2XD4z4W9AWo8SCNSqUXQhnk0Hg9Of0YweMN1TaSZ19pTptamC1a3c9gL7WucagYM1YrEGP7P7kfcpHO7k+pV4GbL5QxgxoYUpg6o+dKWEyTtYRntSlMSLi7BGzz7x1k3H0QhBzJtC0+MbHQ9+rv7s7XqtzoMPRddJZb/0bhb2AoTNvVg1ppSF842d2VmE0whBUYxz2jUYGVtJcAqTriRGSnw==Question 1.3
s+gJTjAbjuG3LRR6OvHejvJJR5zi4kaYK4h7ezqVErhTtr7m/giZCwlndc3mkHJFRgP/34aeA6w6XwSm/oOVacEj71x6YsHYUhxcW8JJeXtf3fOXV8563G7vGIwA9vRi7o0mACognoe+5jn66/AInWPCVFVEKY5PQAMnXEsp6lySJfLeDGL7BdY4nIHpNqS+clQ4C8OZN7BwKb8QJ6+pyjwdcIL0fNSyc4gph+u6iUljFeEBJTq9MiX7uRG4abBgeJOjP9UhED2jvCS1G7Dggg==Worked Example

Try it yourself 2
Question Sequence
Question 1.4
For Questions 4-8:
Vector \(\overrightarrow{A}\) has components, Ax = 2, Ay = 2, Az = 0
Vector \(\overrightarrow{B}\) has components Bx = 7, By = 0, Bz = 0
Question 1.5
cAorbWSVDOL3oecAo3VPO+rIzUVPYPSSA2WXk9xR3vuNFkb+Ee7EbUzxzPjU4iuDXI2xFRQhXxy2ad6HEr+6LQ==Question 1.6
PgMJ1xzEPsMYc7xcnenXwwkzSutam4mz5pecfQ9s3pvxUmQo36/77QYmGUNsW9EtuKVqv6wfRAV/E6xyH2fNRzN/+R0xA5tWsezPWmkNLO2exyfIQuestion 1.7
O4Haxy+Dm/53XrxCZQUdNxvknoE1jqeLG5jzDq2fn05j7qIwbyRYBziWqXOV4OqG4cJRpK53F2d9IOrMV72HFml/GkwVeYFwSV/jNCpgQCqXn33CbNtemb3vY9SQK5yq4qBmJw==Question 1.8
5PwcobH4Np46lJzjqEwguIuy/0xN974BL0qURdc5FMem6qgfkOZrUKMfAoozZMcMYMxUc7SlnQFkpiLYYo0n0JAdtmyBVlAv09pg/KaD6rl6ekTx+sHV8SvdzVMjJdooFMugMUhlVOaHb0CV/yA/+TdmbtPIOgIn5MMexK500twZDjFNSnEQOIYP472PoifxeOYlAkgP1CLTuMWYcRtSB5aghdqKKklM+xX/WdOtzAUsVmX/mrDpwlctJ8qqe4DNbSW/wz4dLPF/l01uztJ8Il0rQve6fYoHFl7hmQ+ygOFPVitd7RYekUrfg/EE3vnVtr28AIjzbGbWKuglhBLHdhhqiFzUOy+yQmSFPDsKDFEWvhigWAILAj2HuZATBcNGkcMLQpBQjyW8t38U4KxGeC57swnPxnF4KnDyY6Iz8RReXzCO0/sOQuUzqWjl+J3KEJ7Yw+L0fB17PF48kCBbKan8HgdvDVqCfFKx2tvmokGZpd2ih4JeZgRtBL42VtLuwtjdd2+XEiV8JlRe2IcM/kpfJzjUDg01TBQKHqIKlsdcd1OJGEofCSiwA8hr0QEvb7+gXSqcMTHfmXkgZhnUkhl02U/hFb9DuNwKx4DDlJ+rPQrCudg3CoRO0ldSLEM7DfPbrcSnbcSn9Hi0A5+fHcxBeRDTwilPfUR1ahz3DyJ1bx3liu9PT3YgwPeBF+r4oJTdodhIem7tubPfLzE8JvWRplZyAjnQ5Vrbg0NSt3CRsL4wrb+m12S7gRY8Rvu97RVmmCpt5kWZBmlCZVGvSzDOZpJCey8TqHIlfH22wb8w1CzB084Ul6SinDQQYr0PLv6M2BBgiwFQkn/i0GIV/koJf900dGljFIHEflIkSayd85e2DHBiMApNnNKRkYDUOBQEpsVwjhfp3WrUv4LqXu2YHV+VJMGpOnuR+ihUSEAqyl13Zuw3HUwP/kZeqtAatGlh8gV5K6aEhNNG+PpsaM6fNz6SHPg4Ohxmk2LKABnobnH3Question 1.9
For Questions 9-12:Calculate the magnitude of the cross product, \(\overrightarrow{A} \times \overrightarrow{B}\) if vector \(\overrightarrow{A}\) has components, Ax = 5, Ay = 5, Az = 0 and vector \(\overrightarrow{B}\) has components Bx = 2, By = 3, Bz = 0
d4uhG5iRbBIf5xsym3XEAKaRcSivKZYtN3Wc9GYJhl2Whe3x5oDrznE0iCN/IBldH8L6ARnD6NPpVoSqezudUUIzEYc=